Recommendation system is a specific type of information filtering technique that attempts to present information items (such as movies, music, web sites, news) that are likely of interest to the user. Traditionally, there are two methods to construct a recommender system a) Content-based recommendation, b) Collaborative Filtering.
The first one analyzes the nature of each item. For instance, recommending poets to a user by performing Natural Language Processing on the content of each poet. Collaborative Filtering, on the other hand has an advantage as it does not require any information about the items or the users themselves. It recommends to the active user, the items, that other users with similar tastes, have liked in the past. i.e collaborative recommender systems (or collaborative filtering systems) try to predict the utility of items for a particular user based on the items previously rated by other users.
There are two categories of CF:
- User-based: measure the similarity between target users and other users
- Item-based: measure the similarity between the items that target users rates/ interacts with and other items
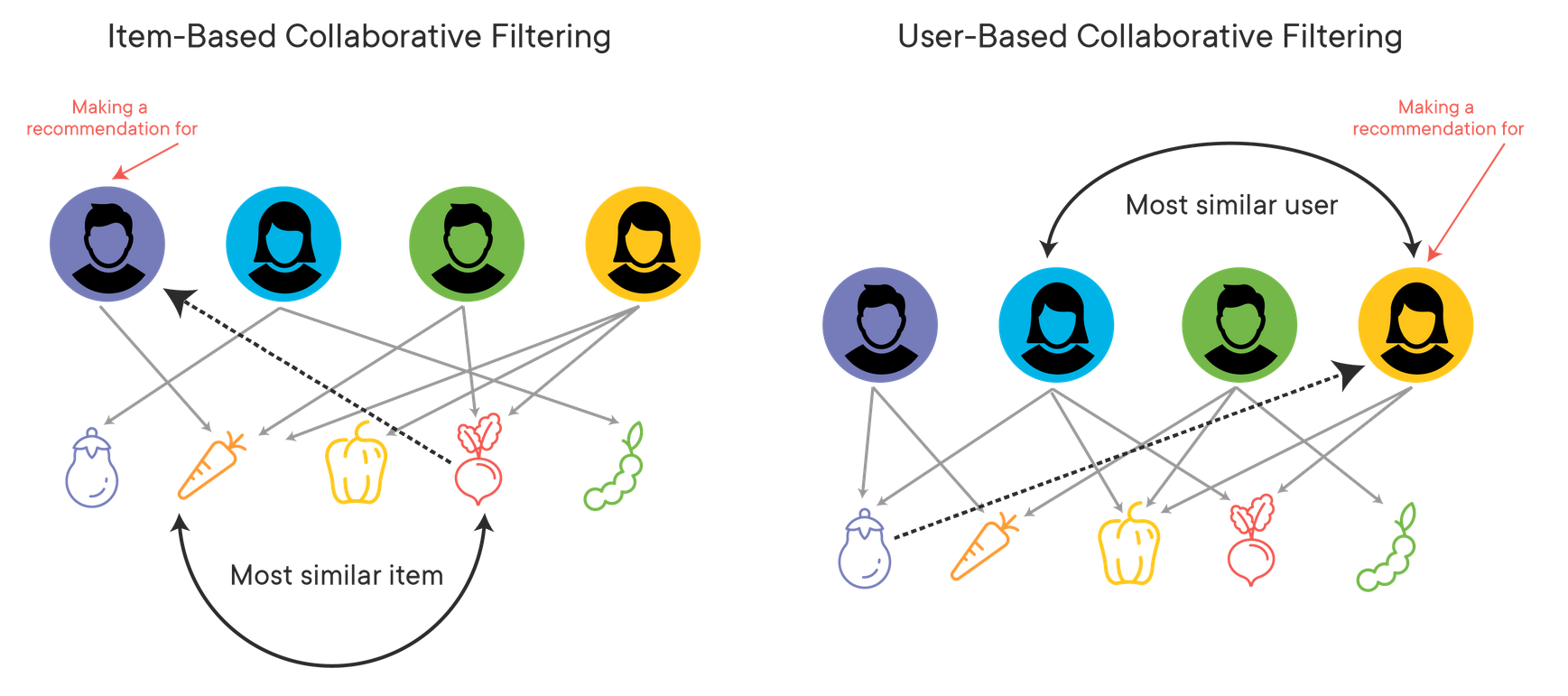
Here is a simple visual example of how these two different comparisons work in the context of buying vegetables in a store. In the left item-based collaborative filtering method, we are trying to come up with a recommendation for Mr. Purple. He knows that he likes carrots, so he wants an item similar to that. To determine the most similar item, we can see what items were rated by other users who also liked carrots. Mr. Green and Ms. Yellow both liked carrots, and they also both liked radishes, making radishes the most similar item, and the one we would recommend to Mr. Purple.
A similar process is conducted for the user-based filtering on the right, where we were trying to make a recommendation for Ms. Yellow. The most similar user to her is Ms. Blue, so we would recommend the item or items that Ms. Blue likes.
Model-Based Collaborative Filtering
Given user data (play counts, ratings, etc.) it is possible to build a sparse user-item relationship matrix, where items could be tracks, purchases, artists or other related entities. From this matrix, we can discover other users with similar tastes (like-minded users) as the active user for which we want to make the prediction. The intuition is that if other users, similar to the active user, already purchased a certain item, then it is likely that the active user will like that item as well. i.e The similarity in taste of two users is calculated based on the similarity in the rating history of the users.
$$
\begin{pmatrix}2&0&0&0&0&6&0&0&0\\0&5&0&0&0&0&1&0&0\\0&0&0&3&0&0&0&0&0\\1&0&0&4&0&0&0&0&0\\0&0&0&0&9&0&0&0&0\\0&0&0&3&0&2&0&0&0\\0&0&8&0&0&0&0&0&0\\0&9&0&0&0&4&0&0&0\\0&1&0&0&0&0&0&0&0\end{pmatrix}
$$
Above is an example of a sparse matrix. all users do not rate all products and services and thus our utility matrix remains highly sparse.
Next, let's look at how a recommendation problem can be translated into a matrix decomposition context. The idea behind such models is that the preferences of users can be determined by a small number of hidden factors. We can call these factors Embeddings. Embeddings are low dimensional hidden factors for items and users. For e.g., say we have 5-dimensional embeddings for both items and users (5 chosen randomly, this could be any number).

One of the most common factorization techniques (for obtaining these embedding matrices) in the context of recommender systems is Singular Value Decomposition. Singular-Value Decomposition or SVD is a common and widely used matrix decomposition method. This approach can reduce the problem from high levels of sparsity. In the figure above, this approach models both users and movies by giving them coordinates in a low dimensional feature space i.e. each user and each item(movie) has a feature vector. And each rating (known or unknown) is modeled as the inner product of the corresponding user and item (movie) feature vectors. In other words, we assume there exist a small number of (unknown) factors that determine (or dominate) ratings, and try to determine the values (instead of their meanings) of these factors based on training data.
Mathematically, “UV-decomposition,” and it is an instance of a more general SVD (singular-value decomposition) approach. Consider movies as a case in point. Most users respond to a small number of features; they like certain genres, they may have certain famous actors or actresses that they like, and perhaps there are a few directors with a significant following. If we start with the utility matrix M, with n rows and m columns(i.e., there are n users and m items), then we might be able to find a matrix U with n rows and d columns and a matrix V with d rows and m columns, such that UV closely approximates M in those entries where M is non-blank. If so, then we have established that there are d-dimensions that allow us to characterize both users and items closely. We can then use the entry in the product UV to estimate the corresponding blank entry in utility matrix M. This process is called UV-decomposition of M.
Collaborative filtering has the disadavantage that it suffers from the cold-start problem, which occurs when it is not possible to make reliable recommendations due to an initial lack of ratings. Also when a new item is available and added, until it has to be rated by substantial number of users, the model is not able to make any personalized recommendations. Similarly, since new users in the system have not yet provided any ratings, they cannot receive any personalized recommendations. overall, we can distinguish three kinds of cold-start problems:new community, new item and new user.
References:
- Mining of Massive datasets - Chapter 9
- https://realpython.com/build-recommendation-engine-collaborative-filtering/#what-is-collaborative-filtering
- https://github.com/learn-co-students/dsc-collaborative-filtering-singular-value-decomposition-houston-ds-060319
- Bobadilla, Jesús, et al. "Recommender systems survey." Knowledge-based systems 46 (2013): 109-132.
- Adomavicius, Gediminas, and Alexander Tuzhilin. "Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions." IEEE transactions on knowledge and data engineering 17.6 (2005): 734-749.
