Prolog was invented in the early seventies by Alain Colmerauer and others at the University of Marseille. Prolog stands for Programmation en Logique (Programming in Logic). Prolog differs from the most common programming languages because it is a declarative langauge. This means that the progammer specifies a goal which is to be achieved and the Prolog interpreter/compiler works out how to achieve it. Traditional programming languages are said to be procedural. This means that the programmer must specify in detail how to solve a problem. In purely declarative languages, the programmer only states what the problem is and leaves the rest to the langauge itself.
In this post we go through an interesting application of prolog. We will write a prolog agent that can find a path from one corner of the maze to the centre position. We want to get there intelligently with few moves as possible. We dont know the initial complete layout of the maze in advance. We assume the agent has sensors that can tell it where the no-go areas are (although to simply things we will hard-code some of the constraints and board position). This allows the agent to explore the space and find a an optimal route.
We describe the maze as follows:
The maze is of size 8 x 7. An intelligent robot is stationed at position (x7,y3). There are walls in this maze (the gray colored grid points). The robot can move in a horizontal or vertical direction (no movement in the diagonal direction is allowed) but must not cross grid points which are marked as a wall, and must not visit grid points that the robot had already visited before (each grid point can be visited at most once). The grid point (x5,y4) is marked to be the goal (the target) for the robot.
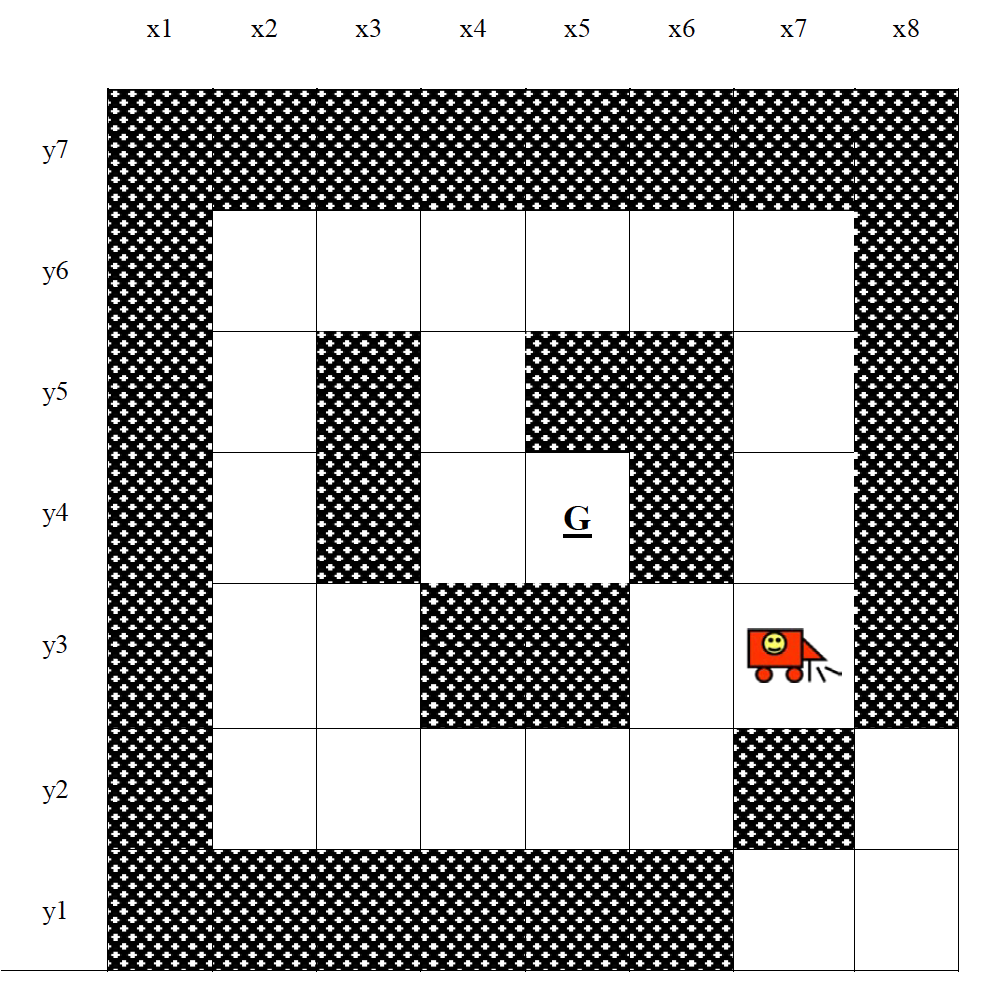
Write a set of rules and facts in SWI-Prolog that represent the maze, starting state of the robot, and the goal state. Then write a predicate roby() which, when called, computes and lists all possible paths which lead the robot from its starting state to the goal state.
Board Representation:
Our Board is represented by valid path points or states that robot can take to reach the goal. We Encode the 8 x 7 board by specifying each single valid co-ordinate the robot is allowed to move to.
validpp(2,6).
validpp(2,5).
validpp(2,4).
validpp(2,3).
validpp(2,2).
validpp(3,6).
validpp(3,3).
validpp(3,2).
validpp(4,6).
validpp(4,5).
validpp(4,4).
validpp(4,2).
validpp(5,6).
validpp(5,4).
validpp(5,2).
validpp(6,6).
validpp(6,3).
validpp(6,2).
validpp(7,6).
validpp(7,5).
validpp(7,4).
validpp(7,3).
validpp(7,1).
validpp(8,2).
validpp(8,1).Encoding Rules for Movement:
moves one position up,down,right or left by incrementing the value of (x,y)
move_pos(PrevX,PrevY,PrevX,Y) :- Y is PrevY+1. % move one position Up
move_pos(PrevX,PrevY,X,PrevY) :- X is PrevX+1. % move one position right
move_pos(PrevX,PrevY,PrevX,Y) :- Y is PrevY-1. % move one position down
move_pos(PrevX,PrevY,X,PrevY) :- X is PrevX-1. % move one position leftGoal Finder Logic:
we recursively check the surrounding states of the robot to see if any of them is a valid state that robot can move to. and we check if the position/state has already been visited by using already visited predicate. In case new a valid position is available and has not been visited before we move the position of the robot by one block and we add it to the Goalpath list and the already visited Path list and continue doing it untill all options have been exhausted
notvisited(_, []) :- !.
notvisited(X, [H|T]) :-
X \= H,
notvisited(X, T).
findGoalPath(X,Y,X,Y,GoalPath,GoalPath).
findGoalPath(PrevX,PrevY,X,Y,AlreadyVisitedPath,GoalPath) :- validpp(NextX,NextY), move_pos(PrevX,PrevY,NextX,NextY),
notvisited(validpp(NextX,NextY),AlreadyVisitedPath),
findGoalPath(NextX,NextY,X,Y,[validpp(NextX,NextY)|AlreadyVisitedPath],GoalPath).
roby():-(findGoalPath(5,4,7,3,[],Path)), append(Path,[validpp(5,4)],Path2),write(Path2), fail.
Usage: Type roby(). in command prompt
