In Information retrieval our starting point is often a term-document matrix constructed by converting the raw text of the corpus. Each row represents a term that occurs in the corpus(and values are its weight) and each column represents a document. This matrix can have a rank in the tens of thousands as well and coming up with a concise representation of this matrix is an interesting challenge.
In this post we briefly explain math concepts behind Topic Modelling approaches like LDA and LSA where we seek to distill a set of topics from a given corpus and assigns each document a level of participation in each topic. LSA discovers the low-dimensional representation using a linear algebra technique called SVD[4]. This approach helps us understand a given corpus of documents and relationships between the words in that corpus.
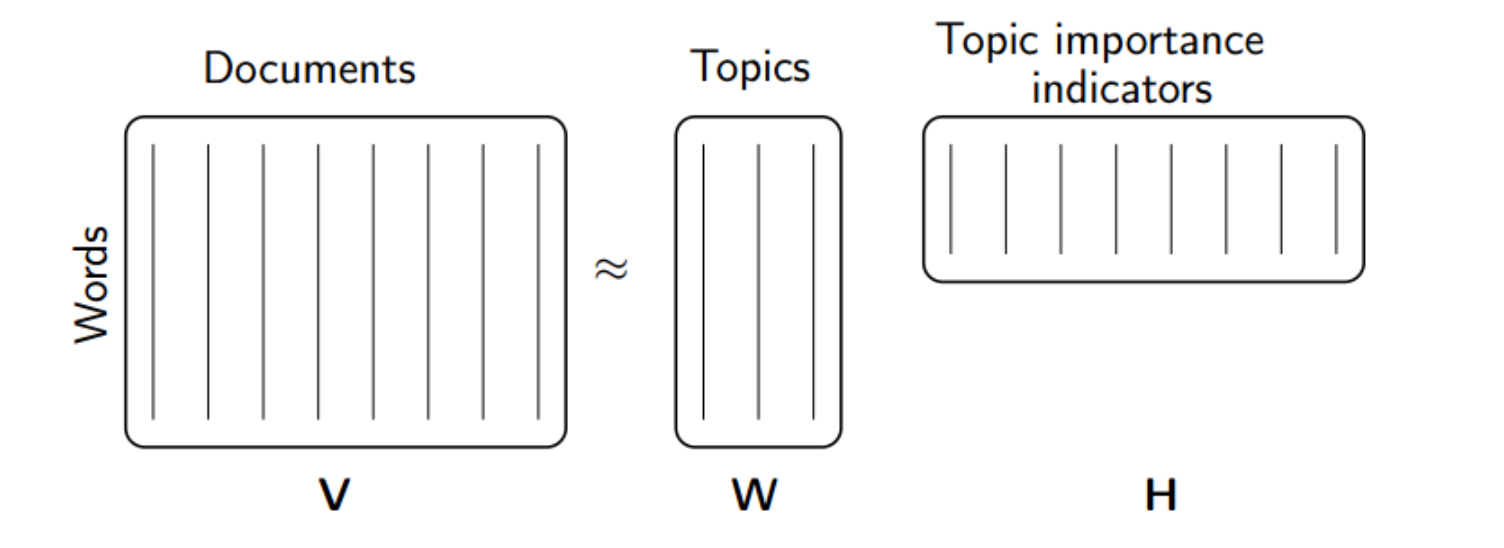
A particularly interesting application of SVD is semantic search (sometimes referred LSA to as latent semantic analysis (LSA)). Using LSA we can match queries to documents based on the semantic meaning of the query, which compared to keyword search is much better as keyword search returns can return irrelevent results in many cases due to synonymy(words having similar meaning) and polysemy(words have more than one meaning). In LSA we use Singular value decomposition to construct a low-rank approximation CK of the term-document matrix, for a value of k that is far smaller than the original rank of C[4].
MLlib contains an implementation of the SVD that can handle large matrices[5]. The SVD takes as input m x n matrix (term-document matrix) and output three that approximately equal it when multiplied together.
M ≈ U S VT
The matrices are:
- U is an m m x k matrix whose columns form an orthonormal basis for the document space.
- S is a k x k diagonal matrix, each of whose entries correspond to the strength of one of the concepts.
- VT is a k x n matrix whose columns form an orthonormal basis for the term space.
Before factorisation we can provide the parameter k which indicates how many factors to keep around.
Spark Implementation:
Spark provides a scalable implementation where MLLib is capable of handling enormous size matrices.
we start by importing relevant libraries.
from __future__ import print_function
# $example on$
from pyspark.ml.feature import HashingTF, IDF, Tokenizer
# $example off$
from pyspark.sql import SparkSession
from pyspark.ml.feature import StopWordsRemover
from pyspark.ml.clustering import LDA
Then Create a session:
if __name__ == "__main__":
spark = SparkSession\
.builder\
.appName("TfIdfExample")\
.getOrCreate()Step 1: PreProcessing
Before we proceed with the modeling we need to pre-process the data. Common approaches for preprocessing as mentioned in literature[1][2][3]:
a. Stop word removal
b. Stemming
c. Term reduction(According to Zipf’s law a large number of terms only appear in one document. Such hapaxes can be removed from the vocabulary because they are of little value in finding communality between documents)
d. Weighting: e.g TF-IDF weighting scheme
Additionally, more advanced, pre-processing tasks such as (proper name recognition; word sense disambiguation; acronym recognition; compound term and collocation detection; feature selection using application-specific domain vocabulary or ontology, information gain, entropy or Bayesian techniques) can be performed to further optimize the indexing process
We will follow a BOW words approach. For a given document, you extract only the unigram words (aka terms) to create an unordered list of words. No POS tag, no syntax, no semantics, no position, no bigrams, no trigrams. Only the unigram words themselves, making for a bunch of words to represent the document.
We start by creating a tiny sample dataset and save it in a file. Next we load in spark:
lines = spark.read.text(in_path).rdd.map(lambda r: json.loads(r[0].encode("utf-8"))["text"].lower())
we can convert the data we just read into a dataframe by the following line:
sentenceData = lines.map(lambda x: (nltk.word_tokenize(x), )).toDF(['words'])
A matrix is formed, wherein each row corresponds to a term that appears in the documents of interest, and each column corresponds to a document. Each element (m,n) in the matrix corresponds to the number of times that the term m occurs in document n.
Tokenize : We should consider implementing stop words earlier before this stage, and in same map function.
tokenizer = Tokenizer(inputCol="raw_sentence", outputCol="words")
wordsData = tokenizer.transform(sentenceData)remove stop words
remover = StopWordsRemover(inputCol="words", outputCol="filtered")
wordsData_updated = remover.transform(wordsData)Step 2: Computing the TF-IDF
Before modeling we need to compute the frequencies for each term within each document and for each term within the entire corpus[5].
CountVectorizer can also be used to compute term frequencies by going through the documents and maping terms to integers which can be converted into a term frequency vector for each document.
cv = CountVectorizer(inputCol="filtered", outputCol="features_CV")
model = cv.fit(wordsData_updated)
df = model.transform(wordsData_updated)df.select("id", "features_CV").show(truncate = False)Compute inverse-document frequencies: We use IDF estimator to first count number of documents in which each term in the corpus appears and then compute scaling factor for each term.
hashingTF = HashingTF(inputCol="filtered", outputCol="rawFeatures", numFeatures=20)
featurizedData = hashingTF.transform(wordsData_updated)
idf = IDF(inputCol="rawFeatures", outputCol="features")
idfModel = idf.fit(featurizedData)
rescaledData = idfModel.transform(featurizedData)
rescaledData.select("id", "features").show(truncate=False) Step 3: Compute SVD matrix
from pyspark.mllib.linalg.distributed import IndexedRow, IndexedRowMatrix, RowMatrix
from pyspark.mllib.linalg import Vectors
mat = RowMatrix(df.rdd.map(lambda v: Vectors.dense(v.rawFeatures.toArray()) ))
svd = mat.computeSVD(2, computeU=True)
#print(mat.rows.collect())
U = svd.U # The U factor is a RowMatrix.
s = svd.s # The singular values are stored in a local dense vector.
V = svd.V # The V factor is a local dense matrix.Indexing: Since Spark doesn't allow us to store the index for search we can use gensim to save the index which we can later use to query the index. we could have computed the whole thing in gensim library doent allow us to scale like spark. see gist for how that can be done. complete code:
Apart from LSA, SVD has many other application in image processing, climatological applications etc. In the next post we will go into the details and see how it can be used to build a semantic search engine where we compute relevance scores between documents. For now here is a quick implementation of LDA which is quite similar to LSA.
(optional alternate) Create a LDA Model

lda = LDA(k=10, maxIter=10)
model = lda.fit(rescaledData)
ll = model.logLikelihood(rescaledData)
lp = model.logPerplexity(rescaledData)
print("The lower bound on the log likelihood of the entire corpus: " + str(ll))
print("The upper bound bound on perplexity: " + str(lp))
topics = model.describeTopics(3)
print("The topics described by their top-weighted terms:")
topics.show(truncate=False)
#show the results
transformed = model.transform(dataset)
transformed.show(truncate=False)References:
[1] https://lirias.kuleuven.be/bitstream/123456789/321960/1/MSI_1114.pdf
[2] http://pages.cs.wisc.edu/~jerryzhu/cs769/text_preprocessing.pdf
[3] Moens, M. F. (2006). Information extraction: Algorithms and prospects in a retrieval context (The Information Retrieval Series 21).
[4] https://nlp.stanford.edu/IR-book/pdf/18lsi.pdf
[5] Ryza, Sandy, et al. Advanced analytics with spark: patterns for learning from data at scale. " O'Reilly Media, Inc.", 2017.APA
