The traveling salesman problem (TSP) is a typical example of a very hard combinatorial optimization problem. The problem is to find the shortest tour that passes through each vertex in a given graph exactly once. We will be use the GA approach to solve this problem. Overall approach of GA's works as below.
Initialize population
while evolution do
Begin
choose parentl and parent2; { selection }
offspring := combination (parentl, parent2);
{crossover} optimize-local (offspring);
{mutation} ifsuited (offspring) survival of the fittest
then perform mutation through swap
end;
Let's Step by Step discuss how each of the functions work.
1. Initialization:
This is done by declaring a 2D array and assigning each member a random value. This results in different combinations of tours Generated. .
2. Evaluation and selection:
GAs use a selection mechanism to select individuals from the population to insert into a mating pool. Individuals from the mating pool are used to generate new offspring , with the resulting offspring forming the basis of the next generation. As the individuals in the mating pool are the ones whose genes are inherited by the next generation, it is desirable that the mating pool be comprised of "good" individuals. A selection mechanism in GAs is simply a process that favours the selection of better individuals in the population for the mating pool[9].
To improve the solutions, each combination in the population is evaluated using a measure of fitness. Using the fitness function we can find the best Tour(combination) that corresponds to the shortest path.
As TSP is a minimization problem so to convert it into maximization problem we have considered fitness function f(x) =1/d, where d calculates cost (or distance/length) of the tour represented by a chromosome.
Normalization: To normalize the results we multiplied it a with a large constant(e.g 10^6). This results the fitness to mostly lie in a range of [0,30]. The fitness function that characterizes each route represents the total length of the route from the first to the last gene (city) moving according to the order of the genes in the route.
Distance Calculation:
If the cities are represented with x and y coordinates in 2D coordinate system, then we calculate the distance between them according the equation:
$$
P Q=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}
$$
To avoid recalculating the distance each time we evaluate the fitness of a tour, we implemented a n x n table which store the distance from every single city to every other city.
2.1 Fitness proportionate selection using Roulette-Wheel:
Roulette wheel selection is a frequently used selection operator in implementation of GA. In this method each individual is assigned a slice of a circular “roulette wheel”, the size of the slice being proportional to the individual’s fitness. The wheel is spun N times, where N is number of individuals in the population. On each spin, the individual under the wheel’s marker is selected to be in the pool of parents for the next generation.
If f(i) is the fitness of individual in the population, its probability of being selected is given by the following equation where is the number of individuals in the population.
$$
p_{i}=\frac{f_{i}}{\sum_{j=1}^{N} f_{j}}
$$
for all members of population
sum += fitness of this individual
end for
for all members of population
probability = sum of probabilities + (fitness / sum)
sum of probabilities += probability
end for
PseduoCode:
This results in each member of the population being assigned a range of probability. After this step we can perform selection:
number = Random between 0 and 1
for all members of population
if number > probability but less than next probability
then you have been selected
2.2 Tournament Selection:
Tournament selection is a method of selecting an individual from a population of individuals in a genetic algorithm. Tournament selection involves running several "tournaments" among a few individuals chosen at random from the population. The winner of each tournament (the one with the best fitness) is selected for crossover. Selection pressure is easily adjusted by changing the tournament size. If the tournament size is larger, weak individuals have a smaller chance to be selected.
3. Generation of offspring population:
To create the next generation, a new set of population called offspring is formed by the execution of genetic operators such as selection, Crossover and mutation. In particular, the crossover operator acts as a main operator and exercises a great influence on the performance of the GA approach, while the mutation operator acts as a background operator.
3.1 Crossover:
Many crossover techniques exist for organisms which use different data structures to store themselves. , a direct swap may not be possible. One such case is when the chromosome is an ordered list, such as an ordered list of the cities to be travelled for the traveling salesman problem. There are many crossover methods for ordered chromosomes. Since Crossover is considered to a very important step in GA, We did an extensive literature review of all the popular and effective techniques that exist. We experimented with the following technique for implementing the cross over function:
PMX crossover Method :
Explained by Gokturk Ucoluk[1], PMX crossover works as follows:
Given two parents s and t, PMX randomly picks a crossover point – like 1-point crossover. The child is then constructed in the following way. Starting with a copy of s, the positions between the crossover points are, one by one, set to the values of t in these positions. To keep the string a valid chromosome the cities in these positions are not just overwritten. To set position p to city c, the city in position p and city c swap positions. Below you see an example of this coding and special crossover technique for two sample permutations: 5, 7, 1, 3, 6, 4, 2 and 4, 6, 2, 7, 3, 1, 5.
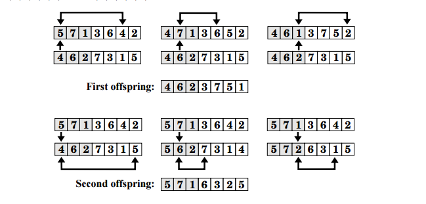
3.2 Mutation:
The swap mutation operates by selecting the two genes within a tour(population member) and then swaping their values. The probability of this operation happening is kept very low[3]. Overall procedure is as follows:
procedure: Applied Genetic Algorithm
initialization
$t \leftarrow 0 ;$
set population size pop_size, number of generation max_gen, probability of crossover $p_{c}$
and probability of mutation $p_{\text {si }}$
initialize parent population $P(t) ;$
evaluate $P(t)$ and select the best solution $\sigma^{e}$ with the minimum objective function among $P(t) ;$
while (no termination criteria) do
regenerate $C(t)$ from $P(t)$ by applying the crossover and mutation operations;
evaluate $C(t)$ and select the current best solution $\sigma$ with the minimum objective value among $C(t)$
update the best solution $\sigma^{8}, i . e_{.},$ if $\sigma<\sigma^{*},$ then $\sigma^{3}=\sigma_{i}$
select $P(t+l)$ from $P(t)$ and $C(t)$;
$t \leftarrow t+1 ;$
end_while.
end_procedure.Conclusion:
Genetic algorithms are an effective way to solve hard problems whose optimum solutions is not easy to find. However when it comes to implementation a lot of GA’s performance depends on the kind of crossover or mutation function you will choose. Through our experimentation we can conclude that Moon Crossover is relatively good method compared to other started crossover methods such as PMX.
Another factor that GA’s performance is detecting and removing duplicates while performing crossover. This step can take up a lot of computation resources and hence its recommended that while comparing different crossover methods we looks at how duplicates are being handled.
code: https://github.com/asjad99/Genetic-Algorithms
References:
[1] Gokt ¨ urk ¨ Uc¸oluk. “Genetic Algorithm Solution of the TSP Avoiding Special Crossover and Mutation”, Department of Computer Engineering Middle East Technical University 06531 Ankara, Turkey.
[2] Davis, L. “Applying Adaptive Algorithms to Epistatic Domains.” Proceedings of the International Joint Conference on Artificial Intelligence, 1985, pp. 162-164
[3] C. Moon et al. “An efficient genetic algorithm for the traveling salesman problem with precedence constraints” European Journal of Operational Research 140 (2002) 606–617
[4] KANCHAN RANI1 & VIKAS KUMAR “SOLVING TRAVELLING SALESMAN PROBLEM USING GENETIC ALGORITHM BASED ON HEURISTIC CROSSOVER AND MUTATION OPERATOR”. IMPACT: International Journal of Research in Engineering & Technology (IMPACT: IJRET) ISSN(E): 2321-8843; ISSN(P): 2347-4599 Vol. 2, Issue 2, Feb 2014, 27-34
[5] Grefenstette, J. “Incorporating Problem Specific Knowledge into Genetic Algorithms.” Genetic Algorithms and Simulated Annealing, edited by Davis L., Morgan Kaufmann, Los Altos, CA, pp. 42-60, 1987.
[6] Goldberg, D.E., and R. Lingle. “Alleles, Loci, and the Traveling Salesman Problem.” Proceedings of the First International Conference on Genetic Algorithms and Their Application, edited by Grefenstette J., Lawrence Erlbaum Associates, Hillsdale, NJ, 1985, pp. 154-159
[7] P. LARRANAGA, C.M.H. KUIJPERS, R.H. MURGA, I. INZA and ˜ S. DIZDAREVIC. Genetic Algorithms for the Travelling Salesman Problem: A Review of Representations and Operators. Artificial Intelligence Review 13: 129–170, 1999. 129 c 1999 Kluwer Academic Publishers
[8] Kylie Bryant, PHD Thesis “Genetic Algorithms and the Traveling Salesman Problem”, December 2000, Department of Mathematics, Harvey Mudd College.
[9] Brad L. Miller , David E . Goldberg. “Genetic Algorithms, Tournament Selection, and the Effects of Noise” Complex Systems 9 (1995) 193- 212.
[17] Syswerda, G. “Schedule Optimization Using Genetic Algorithms.” Handbook of Genetic Algorithms, edited by Davis L., Van Nostrand Reinhold, New York, 1991, pp. 332-349
